Sparse Sinkhorn Attention 论文精读

在 Transformer 的 self-attention 计算规则中，每个 token 需要与其他所有 token 点乘进行计算。这样的计算量非常大，且存在部分无意义的计算。

作者希望每个 token 只与某一相关性最大的部分的 token 进行计算，因此，作者将文本按每 ( l_B ) 个进行分块，然后训练了一个函数 ( P(X) ) 用来计算出对于每一个块与它相关性最大的块。

具体的计算规则如下：

1. 首先，对于输入 ( X ) (长度为 L)，将其分块，并对每个块内的 token 进行求和，计算出 ( X’ ) (长度为 ( N_B = \frac{L}{l_B} ))。其中 ( \psi ) 是一个 ( \mathbb{R}^{L \times d} \rightarrow \mathbb{R}^{N_B \times d} ) 的函数，( d ) 是编码长度。

   

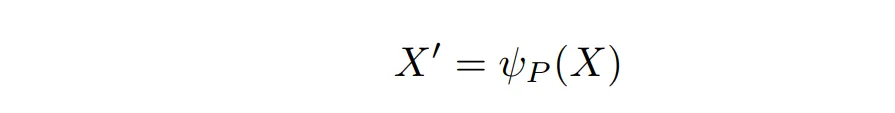
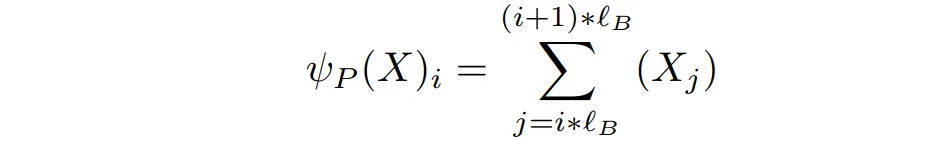
   由于只求和一个块内的 token 可能不能表达其含义，另一种方式是通过计算 ( \psi )。

   

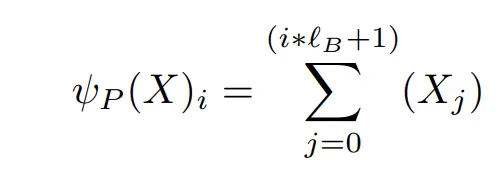
2. 接下来训练 ( P(X) )。（其中 ( \sigma ) 为 ReLU，( W_P ) 是一个 ( d \times d ) 的矩阵，( W_Q ) 是一个 ( d \times N_B ) 的矩阵。）

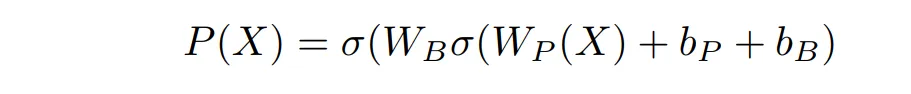
1. 由于我们需要求出一个排序矩阵，我们需要让结果是一个 doubly stochastic（矩阵非负，且行列和都是 1）。因此我们需要对结果进行规范化。（( R ) 为 ( P(X) ) 的结果，( K ) 为选定的超参，( F_r, F_c ) 是行和列的归一化，整个过程就是不断的行归一再列归一。）

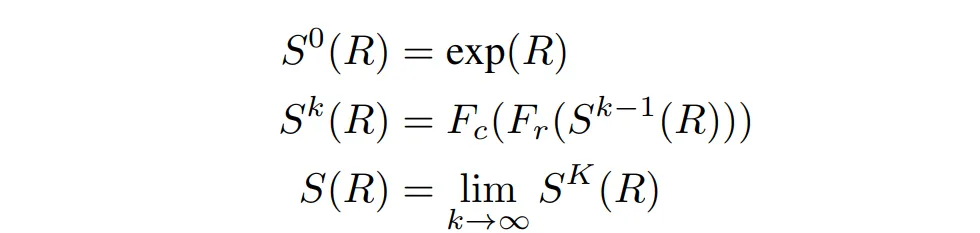
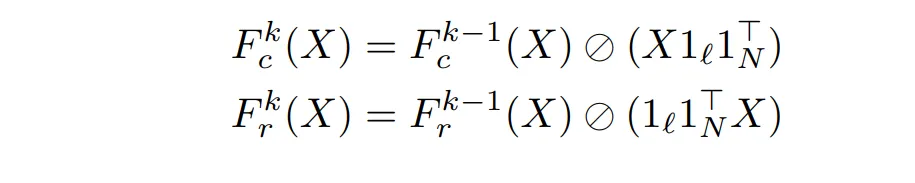
由于归一化中有除法，所以改变为 exp 后做减法：

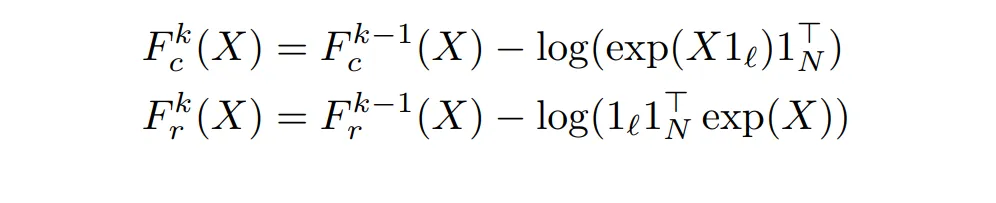
在 mask 下的计算规则如下：

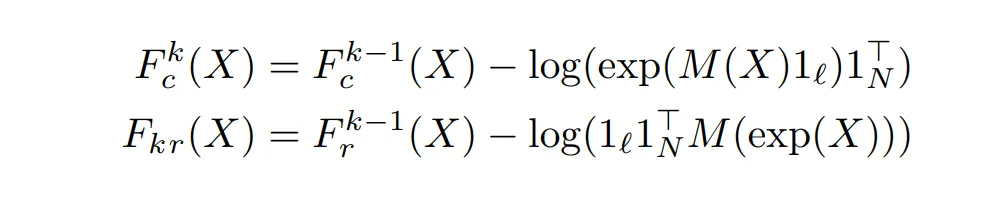
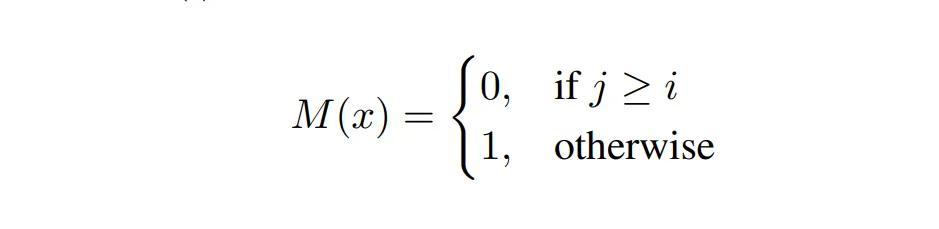
将原本分块的结果乘上 ( R ) 就相当于进行了一次排序。（为了使 ( S(X) ) 近似双重随机排列矩阵，我们利用了 Gumbel 分类的重新参数化技巧。具体地，我们在排序操作中注入 Gumbel 噪声，即 ( S(X) = S\left(\frac{X+\epsilon}{\tau}\right) )，其中 ( \epsilon ) 是注入的标准独立同分布的 Gumbel 噪声，( \tau ) 是温度超参数。直观地说，降低温度使 ( S(X) ) 更接近具有离散 1 和 0 的排列矩阵。）

将块进行重排之后，原本第 ( i ) 个块只需要和它自己以及重排后第 ( i ) 个块计算 attention。

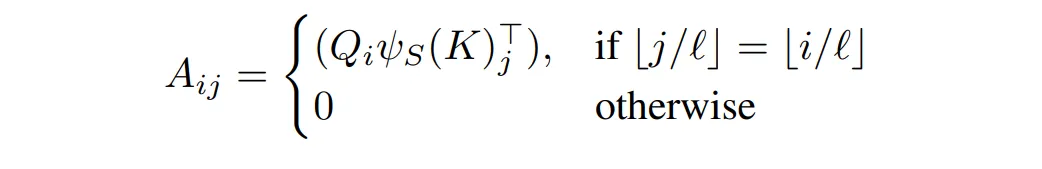
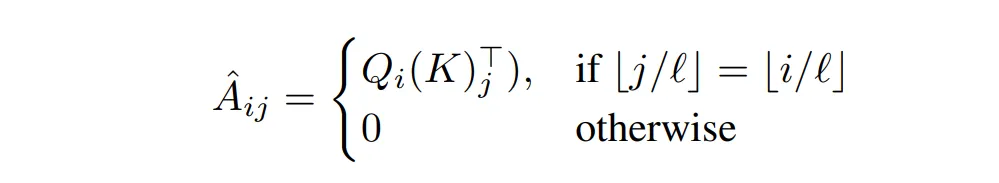
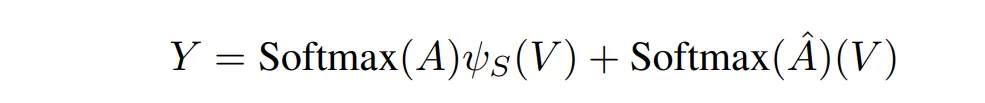论文还提出了一种混合计算方式，即一般的 attention 值再加上块内相乘的计算结果。